Monsieur Descartes and many other clever mathematicians have thought that the quantity of motion, that is to say the velocity multiplied by the mass1 of the moving body, is exactly equivalent to the moving force, or to speak in mathematical terms that the force varies as the velocity multiplied by the mass. Now it is reasonable that the same force is always preserved in the universe. So also, looking to phenomena, it will be readily seen that a mechanical perpetual motion is impossible, because the force in such a machine, being always diminished a little by friction and so ultimately destined to be entirely spent, would necessarily have to recoup its losses, and consequently would keep on increasing of itself without any new impulsion from without; and we see furthermore that the force of a body is diminished only in proportion as it gives up force, either to a contiguous body or to its own parts, in so far as they have a separate movement. The mathematicians to whom I have referred think that what can be said of force can be said of the quantity of motion. In order, however, to show the difference I make two suppositions: in the first place, that a body falling from a certain height acquires a force enabling it to remount to the same height, provided that its direction is turned that way, or provided that there are no hindrances. For instance, a pendulum will rise exactly to the height from which it has fallen, provided the resistance of the air and of certain other small particles do not diminish a little its acquired force.
I suppose in the second place that it will take as much force to lift a body. A weighing one pound to the height CD, four feet, as to raise a body B weighing four pounds to the height EF, one foot.
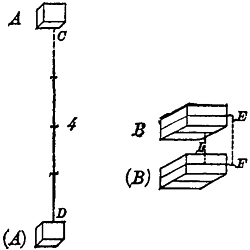
These two suppositions are granted by our new philosophers. It is therefore manifest that the body A falling from the height CD acquires exactly as much force as the body B falling from the height EF, for the body B at F, having by the first supposition sufficient force to return to E, has therefore the force to carry a body of four pounds to the distance of one foot, EF. And likewise the body A at D, having the force to return to C, has also the force required to carry a body weighing one pound, its own weight, back to C, a distance of four feet. Now by the second supposition the force of these two bodies is equal. Let us now see if the quantity of motion is the same in each case. It is here that we will be surprised to find a very great difference, for it has been proved by Galileo that the velocity acquired by the fall CD is double the velocity acquired by the fall EF, although the height is four times as great. Multiplying, therefore, the body A, whose mass is 1, by its velocity, which is 2, the product or the quantity of movement will be 2, and on the other hand, if we multiply the body B, whose mass is 4, by its velocity, which is 1, the product or quantity of motion will be 4. Hence the quantity of the motion of the body A at the point D is half the quantity of motion of the body B at the point F, yet their forces are equal, and there is therefore a great difference between the quantity of motion and the force. This is what we set out to show. We can see therefore how the force ought to be estimated by the quantity of the effect which it is able to produce, for example by the height to which a body of certain weight can be raised. This is a very different thing from the velocity which can be imparted to it, and in order to impart to it double the velocity we must have double the force. Nothing is simpler than this proof and Monsieur Descartes has fallen into error here, only because he trusted too much to his thoughts even when they had not been ripened by reflection. But it astonishes me that his disciples have not noticed this error, and I am afraid that they are beginning to imitate little by little certain Peripatetics whom they ridicule, and that they are accustoming themselves to consult rather the books of their master, than reason or nature.
XVIII. The distinction between force and the quantity of motion is, among other reasons, important as showing that we must have recourse to metaphysical considerations in addition to discussions of extension if we wish to explain the phenomena of matter.
This consideration of the force, distinguished from the quantity of motion is of importance, not only in physics and mechanics for finding the real laws of nature and the principles of motion, and even for correcting many practical errors which have crept into the writings of certain able mathematicians, but also in metaphysics it is of importance for the better understanding of principles. Because motion, if we regard only its exact and formal meaning, that is, change of place, is not something entirely real, and when several bodies change their places reciprocally, it is not possible to determine by considering the bodies alone to which among them movement or repose is to be attributed, as I could demonstrate geometrically, if I wished to stop for it now. But the force, or the proximate cause of these changes is something more real, and there are sufficient grounds for attributing it to one body rather than to another, and it is only through this latter investigation that we can determine to which one the movement must appertain. Now this force is something different from size, from form or from motion, and it can be seen from this consideration that the whole meaning of a body is not exhausted in its extension together with its modifications as our moderns persuade themselves. We are therefore obliged to restore certain beings or forms which they have banished. It appears more and more clear that although all the particular phenomena of nature can be explained mathematically or mechanically by those who understand them, yet nevertheless, the general principles of corporeal nature and even of mechanics are metaphysical rather than geometric, and belong rather to certain indivisible forms or natures as the causes of the appearances, than to the corporeal mass or to extension. This reflection is able to reconcile the mechanical philosophy of the moderns with the circumspection of those intelligent and well-meaning persons who, with a certain justice, fear that we are becoming too far removed from immaterial beings and that we are thus prejudicing piety.
XIX. The utility of final causes in Physics.
As I do not wish to judge people in ill part I bring no accusation against our new philosophers who pretend to banish final causes from physics, but I am nevertheless obliged to avow that the consequences of such a banishment appear to me dangerous, especially when joined to that position which I refuted at the beginning of this treatise. That position seemed to go the length of discarding final causes entirely as though God proposed no end and no good in his activity, or as if good were not to be the object of his will. I hold on the contrary that it is just in this that the principle of all existences and of the laws of nature must be sought, hence God always proposes the best and most perfect. I am quite willing to grant that we are liable to err when we wish to determine the purposes or councils of God, but this is the case only when we try to limit them to some particular design, thinking that he has had in view only a single thing, while in fact he regards everything at once.
1 comment