Everyday objects, like cars and speeding cricket balls, have such high masses that their quantum wavelengths are vastly smaller than their sizes and we can forget about quantum influences when driving cars or watching cricket matches.
By contrast, general relativity was always necessary when dealing with situations where anything travelled at a speed at, or close to, the speed of light or where gravity is very strong. It is used to describe the expansion of the universe and the behaviour of extreme situations like the formation of black holes. However, gravity is very weak compared with the forces that bind atoms and molecules together and far too weak to have any effect on the structure of atoms or sub-atomic particles.
As a result of these properties, quantum theory and gravitation govern different kingdoms that have little cause to talk to one another. This is fortunate. No one knows how to join the two theories together seamlessly to form a new, bigger and better edition that could deal with quantum aspects of gravity. All the candidates remain untested. But how can we tell when such a theory is essential? What are the limits of quantum theory and Einstein's general relativity theory? Fortunately, there is a simple answer and Planck's units tell us what it is.
Suppose we take the whole mass inside the visible Universe19 and determine its quantum wavelength. We can ask when this quantum wavelength of the visible Universe exceeds its size. The answer is when the Universe is smaller than the Planck length in size (10–33 cm), less than the Planck time in age (10–43 secs), and hotter than the Planck temperature (1032 degrees). Planck's units mark the boundary of applicability of our current theories. To understand what the world is like on a scale smaller than the Planck length we have to understand fully how quantum uncertainty becomes entangled with gravity. To understand what might have gone on close to the event that we are tempted to call the beginning of the Universe or the beginning of time we have to penetrate the Planck barrier. The constants of Nature mark out the frontiers of our existing knowledge and show us where our theories start to overreach themselves.
In the recent attempts that have been made to create a new theory to describe the quantum nature of gravity a new significance has emerged for Planck's natural units. It appears that the concept we call ‘information’ has a deep significance in the universe. We are used to living in what is sometimes called ‘the information age’. Information can be packaged in more electronic forms, dispatched more quickly and received more easily than ever before. The progress we have made in processing information quickly and cheaply is commonly displayed in a form which enables us to check the prediction of Gordon Moore, the founder of Intel, called Moore's Law (see Figure 3.2). In 1965, Moore noticed that the area of a transistor was being halved approximately every 12 months. In 1975 he revised this halving time to 24 months. This is ‘Moore's Law’: that every 24 months you get about twice as much computer circuitry, running at twice the speed, for the same price because the cost of integrated circuit remains roughly constant.
The ultimate limits that we can expect to be placed upon information storage and processing rates are imposed by the constants of Nature. In 1981, an Israeli physicist, Jacob Bekenstein, made an unusual prediction that was inspired by what he knew from the study of black holes. He calculated that there is a maximum amount of information that can be stored inside any volume. This should not surprise us. What should is that the maximum value is just determined by the surface area surrounding the volume, not the volume itself. The maximum number of bits of information that can be stored in a volume is just given by computing its surface area in Planck units. Suppose that the region is spherical. Then its surface area is just proportional to the square of its radius, while the Planck area is proportional to the Planck
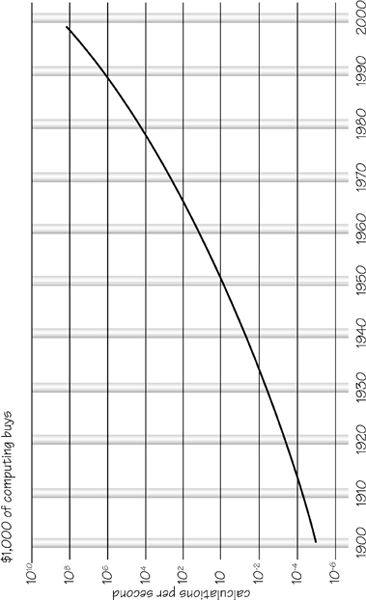
Figure 3.2Moore's Law shows the evolution of computer processing speed versus time. Every two years the number of transistors that can be packed into a given area of integrated circuit doubles. This biennial halving of transistor size means that the computing speed of each transistor doubles every two years for the same cost.
length squared (10–66 cm2). The total number of bits in a sphere of radius R centimetres is therefore just given by 1066 × R2.
1 comment