Le monde comme volonté et comme représentation Read Online

De même, le théorème de Pythagore nous apprend une « qualité occulte » du triangle rectangle ; la démonstration boiteuse et même captieuse d’Euclide nous abandonne au pourquoi, tandis que la simple figure, déjà connue, que nous reproduisons, nous fait entrer du premier coup, et bien plus profondément que la démonstration, au cœur même de la question ; elle nous amène à une plus intime conviction de la nécessité de cette propriété, et de sa liaison avec l’essence même du triangle rectangle :

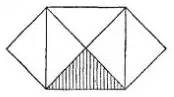
Même dans le cas où les côtés du triangle sont inégaux, on doit arriver à une semblable démonstration, et en général dans le cas de toute vérité géométrique possible. La raison en est que la découverte de ces vérités procède chaque fois d’une semblable nécessité intuitive et que la démonstration ne vient s’y ajouter qu’après. Ainsi, on n’a besoin que d’une analyse de la marche de la pensée, ou de la première découverte d’une vérité géométrique, pour en connaître intuitivement la nécessité. C’est surtout la méthode analytique que je désirerais pour l’exposition des mathématiques, au lieu de la méthode synthétique, dont s’est servi Euclide. Il en résulterait, pour les vérités mathématiques un peu compliquées, de grandes difficultés sans doute, mais on pourrait en venir à bout. Déjà, en Allemagne, on commence, çà et là, à changer le mode d’exposition des sciences mathématiques et à préférer la méthode analytique. La plus énergique tentative en ce sens est celle de M. Rosack, professeur de mathématique et de physique au collège de Nordhausen, qui, dans le programme des examens du 6 avril 1852, a inséré un projet détaillé pour l’enseignement de la géométrie suivant mes principes.

Pour amender la méthode, en mathématiques, il faudrait exiger, avant tout, qu’on abandonnât ce préjugé qui consiste à croire que la vérité démontrée est supérieure à la connaissance intuitive, ou, en d’autres termes, que la vérité logique, reposant sur le principe de contradiction, doit avoir le pas sur la vérité métaphysique, qui est immédiatement évidente et dans laquelle rentre l’intuition pure de l’espace.

La certitude absolue et indémontrable réside dans le principe de raison ; car ce principe, sous ces différentes formes, constitue le moule commun de toutes nos connaissances. Toute démonstration est un retour à ce principe ; elle consiste à indiquer, pour un cas isolé, le rapport qui existe entre les représentations et que le principe de raison exprime. Ainsi, il est le principe de toute explication, et, par conséquent, n’est susceptible ni n’a besoin d’aucune explication particulière, puisque toute explication le suppose et n’a de sens que par lui. Mais aucune de ses formes n’est supérieure aux autres, il est également certain comme principe de la raison d’être, du devenir, de l’agir ou du connaître. Le rapport de cause à effet est nécessaire, sous l’une comme sous l’autre de ses formes ; c’est même l’origine, comme l’unique signification du concept de nécessité. Il n’y a pas d’autre nécessité que celle de l’effet lorsque la cause est donnée, et il n’y a pas de cause qui n’entraîne la nécessité de son effet. Aussi sûre est la conséquence exprimée dans une conclusion qu’on a déduite du principe de raison contenu dans les prémisses, aussi sûrement le principe d’être dans l’espace entraîne ses conséquences dans l’espace. Dès que j’ai bien saisi, dans une intuition, le rapport du principe à la conséquence, j’ai atteint à une certitude aussi complète que n’importe quelle certitude logique. Or chaque théorème de géométrie exprime ce rapport, au même titre que l’un des douze axiomes ; il est une vérité métaphysique, et, comme tel, aussi immédiatement certain que le principe de contradiction lui-même, qui est une vérité métalogique et le fondement commun de toute démonstration logique. Celui qui nie la nécessité intuitive des rapports d’espace, exprimés par un théorème, peut contester les axiomes aussi bien que la conclusion d’un syllogisme, que dis-je ? le principe de contradiction lui-même : car tout cela, ce sont des rapports également indémontrables, immédiatement évidents et perceptibles a priori. Par conséquent, vouloir déduire la nécessité des rapports d’espace perceptible intuitivement à l’aide d’une démonstration logique basée sur le principe de contradiction, c’est vouloir tout justement donner en fief à quelqu’un un pays qu’il possède comme suzerain. C’est cependant ce qu’a fait Euclide. Ses axiomes seuls (et cela forcément) reposent sur l’évidence immédiate ; toutes les vérités géométriques suivantes sont prouvées logiquement, – c’est-à-dire, ces axiomes une fois posés, par l’accord avec les conditions établies dans le théorème donné, ou avec un théorème antérieur, ou par la contradiction qui naîtrait entre l’opposé du théorème et les données admises, à savoir ou les axiomes, ou les théorèmes précédents, ou la proposition elle-même. Mais les axiomes eux-mêmes ne sont pas plus immédiatement évidents que tout autre théorème de géométrie ; ils sont plus simples, vu leur contenu borné. Quand on interroge un criminel, on note ses réponses pour tirer la vérité de leur comparaison. Mais c’est un pis-aller, auquel on ne saurait se tenir lorsqu’on peut se convaincre immédiatement de la vérité de chaque réponse, d’autant plus que l’individu en question a pu mentir avec suite depuis le commencement. Cette première méthode est cependant celle d’Euclide, quand il interroge l’espace. Il part de ce principe juste que la nature, sous sa forme essentielle, l’espace, est continue, et que, par conséquent, – comme les parties de l’espace sont dans un rapport de cause à effet, – aucune détermination particulière ne peut être autre qu’elle n’est, sans se trouver en contradiction avec toutes les autres. Mais c’est un détour pénible et insuffisant. On en arrive ainsi à préférer la connaissance indirecte à la connaissance directe, qui est aussi certaine, à séparer au grand détriment de la science, le fait de savoir que telle chose est, du fait de connaître, son pourquoi à détourner l’élève de toute vue des lois de l’espace ; on le déshabitue de descendre par lui-même jusqu’aux principes et de saisir les rapports des choses, en le poussant à se contenter de la connaissance historique que telle chose existe. Le mérite tant vanté de cette méthode, qui exerce, dit-on, la pénétration de l’esprit, consiste en ce que l’élève s’habitue à tirer des conclusions, c’est-à-dire à appliquer le principe de contradiction, mais surtout à faire des efforts de mémoire pour retenir toutes les données dont il a à comparer la concordance.

Il est à remarquer d’ailleurs que cette méthode de démonstration n’a été appliquée qu’à la géométrie, et non à l’arithmétique. Ici la vérité sort vraiment de la seule intuition, qui consiste dans l’acte de compter. Comme l’intuition du nombre n’existe que dans le temps, – et par conséquent n’a besoin d’être présentée par aucun schème sensible, comme les figures géométriques, or ne peut plus soupçonner ici que l’intuition est seulement empirique, et partant sujette à l’illusion, soupçon qui seul a pu introduire en géométrie la démonstration logique. Comme le temps n’a qu’une dimension, compter est l’unique opération arithmétique ; c’est à elle que se ramènent toutes les autres.