Le monde comme volonté et comme représentation Read Online

Or cet acte de compter n’est pas autre chose qu’une intuition a priori, à laquelle on ne peut pas hésiter à se reporter ; elle seule, en dernière analyse, vérifie tout le reste, calcul ou équation. On ne prouve pas, par exemple, que

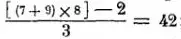
mais on se reporte à la pure intuition dans le temps, si bien que chaque proposition devient un axiome. Il n’y a pas en arithmétique cette masse de preuves qui encombre la géométrie ; la méthode y consiste, comme en algèbre, à abréger l’opération de compter. Notre intuition des nombres dans le temps, comme nous l’avons fait voir, ne va guère au-delà de dix ; pour aller plus loin, il faut fixer dans un mot un concept abstrait du nombre qui représente l’intuition ; il est clair qu’alors celle-ci n’a plus lieu réellement, mais est simplement indiquée avec une grande précision. Cependant l’évidence intuitive de chaque calcul est rendue possible, grâce à l’ordre des nombres, qui permet de représenter toujours de plus grands nombres par l’adjonction des mêmes petits ; cette évidence se retrouve même dans le cas où l’abstraction est poussée si loin, que non seulement les nombres, mais des quantités indéterminées et des opérations entières n’existent que pour la pensée in abstracto, et ne sont exprimées qu’à cet effet ; telle est l’expression 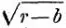 ; on n’effectue pas ces opérations, on se borne a en poser le signe.

On aurait autant de raisons et des raisons aussi sûres de procéder en géométrie comme en arithmétique, et d’y asseoir la vérité sur l’intuition pure a priori. En réalité, c’est la nécessité reconnue intuitivement, conformément au principe de raison d’être, qui donne à la géométrie sa grande évidence ; c’est sur elle que repose la certitude qu’ont ses propositions dans la conscience de chacun : ce n’est pas du tout sur la preuve logique, – véritable béquille, – toujours étrangère à l’objet même qu’on étudie, vite oubliée dans la plupart des cas, sans que la conviction de l’élève en souffre, et qu’on pourrait tout à fait abandonner, sans que l’évidence de la géométrie en fût diminuée, puisque cette évidence est indépendante d’elle, et que la preuve, en définitive, se borne à démontrer une chose dont un autre mode de connaissance nous a déjà parfaitement convaincus. Elle ressemble à un lâche soldat qui achève un ennemi blessé et se vante ensuite de l’avoir tué(27).

Après toutes ces considérations, personne ne doutera, j’espère, que l’évidence en mathématique, – qui est devenue le modèle et le symbole de toute évidence, – dérive, par son essence même, non pas d’une démonstration, mais d’une intuition immédiate, qui là, comme partout, est le fondement et la source de toute vérité. Cependant l’intuition, qui est la base des mathématiques, l’emporte de beaucoup sur toutes les autres, et particulièrement sur l’intuition empirique. Comme elle est a priori, et avec cela indépendante de l’expérience toujours partielle et successive, tout lui est également prochain, et l’on peut à volonté partir du principe ou de la conséquence. Ce qui lui donne sa grande sûreté, c’est qu’en elle la conséquence est connue dans le principe, – ce genre de connaissance est le seul qui ait le caractère de la nécessité : par exemple, l’égalité des côtés est reconnue et fondée à la fois sur l’égalité des angles ; au contraire, l’intuition empirique et la majeure partie de l’expérience vont de l’effet à la cause ; d’autre part, ce dernier mode de connaissance n’est pas infaillible, car l’effet n’est reconnu nécessaire qu’après que la cause est donnée, et non la cause reconnue par l’effet, puisque le même effet peut résulter de causes différentes. Ce dernier mode de connaissance n’est jamais qu’inductif. L’induction consiste, quand plusieurs effets indiquent la même cause, à pour tenir cette cause certaine ; mais, comme on ne peut réunir l’ensemble des cas, la vérité n’est jamais inconditionnellement certaine. Or c’est là la vérité inhérente à toute connaissance venue par l’intuition sensible, et à presque toute l’expérience. L’affection d’un sens détermine l’entendement à conclure de l’effet à la cause ; mais comme conclure de l’effet à la cause n’est jamais infaillible, il s’ensuit que la fausse apparence, sous la forme d’illusion des sens, est souvent possible, et même se produit, comme nous l’avons déjà montré. Quand plusieurs sens, ou tous les cinq à la fois, sont affectés de manière à indiquer la même cause, alors la possibilité d’erreur devient minime, sans toutefois disparaître complètement : car, dans certains cas, avec de la fausse monnaie par exemple, on trompe tous les sens à la fois. C’est ce qui arrive pour toute notre connaissance empirique, et par suite aussi pour toute science naturelle, sauf en ce qu’elle a de pur (ce que Kant appelle le côté métaphysique). Dans les sciences naturelles, on reconnaît également les causes par les effets ; aussi reposent-elles toutes sur des hypothèses, qui se montrent souvent fausses et font place successivement à des hypothèses plus justes. Ce n’est que lorsqu’on institue intentionnellement des expériences, que l’on apprend à connaître l’effet par la cause : c’est là la vraie voie ; mais les expériences elles-mêmes ne sont que la suite des hypothèses. Cela nous explique pourquoi aucune branche des sciences naturelles, ni physique, ni astronomie, ni physiologie, n’a pu être découverte d’un seul coup, comme les mathématiques ou la logique, et pourquoi il a fallu et il faut encore les expériences réunies et comparées de bien des siècles pour en assurer le progrès. Ce n’est qu’une confirmation expérimentale multipliée qui peut donner à l’induction sur laquelle repose l’hypothèse une perfection telle qu’elle puisse, pour la pratique, tenir lieu de certitude et enlever peu à peu à l’hypothèse ses chances originelles d’erreur ; c’est exactement ce qui arrive, en géométrie, pour l’incommensurabilité entre une courbe et une droite, ou, en arithmétique, pour le logarithme, qu’on n’obtient jamais qu’avec une certitude approchée ; car de même qu’au moyen d’une fraction infinie on peut pousser la quadrature du cercle et la recherche du logarithme aussi près qu’on voudra de l’exactitude absolue, de même de nombreuses expériences peuvent rapprocher l’induction, ou connaissance de la cause par l’effet, de l’évidence mathématique, ou connaissance de l’effet par sa cause ; et ce rapprochement peut être poussé, sinon à l’infini, du moins assez loin pour que la chance d’erreur devienne négligeable. Elle existe cependant, par exemple quand nous concluons d’un grand nombre de cas à la totalité des cas, c’est-à-dire à la cause inconnue dont cette totalité dépend. Quelle conclusion de ce genre peut nous sembler plus sûre que celle-ci : « tous les hommes ont le cœur à gauche » ? Il y a cependant des cas isolés, extrêmement rares sans doute, où l’on constate que le cœur est à droite. – Ainsi l’intuition sensible et les sciences expérimentales participent au même genre d’évidence. La supériorité qu’ont les mathématiques, la science naturelle pure et la logique, comme connaissance a priori, repose uniquement sur ce fait que la partie formelle des connaissances sur laquelle se fonde toute apriorité est donnée tout entière en une fois, et que, par conséquent, c’est là seulement qu’on peut aller de la cause à l’effet, tandis qu’ailleurs on remonte la plupart du temps de l’effet à la cause. Du reste, le principe de causalité ou principe de raison du devenir, qui règle la connaissance empirique, est en lui-même aussi sûr que toutes les autres formes du principe de raison, auxquelles sont soumises les sciences a priori, mentionnées plus haut. Les preuves logiques tirées de concepts, ainsi que leurs conclusions, participent au privilège de l’intuition a priori, qui est d’aller de la cause à l’effet, c’est-à-dire qu’au point de vue formel elles sont infaillibles. Cela n’a pas médiocrement contribué au prestige de la démonstration apriori. Mais cette infaillibilité est toute relative ; car elle fait tout rentrer, par subsomption, dans les principes premiers de la science : ce sont eux qui contiennent tout le fonds de la vérité scientifique ; ils n’ont pas besoin d’être prouvés, mais ils doivent se fonder sur l’intuition, qui est pure dans les quelques sciences a priori que nous avons citées, mais ailleurs toujours empirique et élevée au général par voie d’induction. Si donc, dans les sciences expérimentales, on a prouvé le général par le particulier, le général, à son tour, a tiré du particulier tout ce qu’il contient de vérité ; il n'est qu’un grenier à provisions, et non un terrain qui produit de son propre fonds.

Voilà pour le fondement de la vérité. Quant à l’origine et à la possibilité de l’erreur, on en a tenté bien des explications, depuis les solutions toutes métaphoriques de Platon (le pigeonnier où l’on saisit un autre pigeon que celui qu’on voulait, etc.