In addition, the incorporation of Boltzmann's constant, k – which simply converts units of energy into units of temperature – allowed him also to define a natural temper-ature.45 Planck's units are the only combinations of these constants which can be formed with the dimensions of mass, length, time and temperature. Their values are not very different from Stoney's:
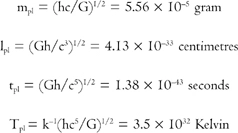
Again, we see a contrast between the small, but not outrageously small natural unit of mass and the fantastically extreme natural units of time, length and temperature.46 These quantities had a superhuman significance for Planck. They cut into the bedrock of physical reality:
‘These quantities retain their natural significance as long as the law of gravitation and that of the propagation of light in a vacuum and the two principles of thermodynamics remain valid; they therefore must be found always to be the same, when measured by the most widely differing intelligences according to the most widely differing methods.’
He alludes in his closing words to the idea of observers elsewhere in the Universe defining and appreciating these quantities in the same way as ourselves.47
For the time, there was something quite striking about Planck's units, as there was also about Stoney's. They entwined gravity with the constants governing electricity and magnetism. Gravity had always been a largely uneventful branch of physics. Newton had apparently found the law of gravity and very few questions were asked about it thereafter. True, there were annoying small discrepancies between its predictions and the observed wobble of the planet Mercury as it orbited close to the Sun. Some had even suggested making a tiny change to Newton's law to explain it but most astronomers expected that small effects from the non-spherical shape of the Sun or errors in the observations might rescue Newton. It seemed to be a finished story.
By contrast, there was continual progress and debate about the laws of electricity and magnetism. They began looking like separate laws for static electricity (that makes your hair stand on end), dynamic electricity (that makes currents flow), and magnetism. But gradually the two electricities were found to be different complexions of one electric force. And then Maxwell showed that electricity and magnetism were really different sides of the same coin: moving magnets could make electrical currents flow and electric currents could create magnetic forces. But never did gravity seem to impinge upon electricity and magnetism or the behaviour of atoms and molecules. As a result we see that there existed a very different view to that of Planck and Stoney about natural units. The physicist Paul Drude, a leading contributor to the study of electromagnetic waves, optics and materials, held the prestigious professorship of physics at Leipzig. In 1897 Drude proposed48 a system of absolute units of mass, length and time that were tied to the properties of the aether that was then believed to permeate all space. His choice of standards were the velocity of light, and the average distance travelled by the particles of the aether before they interacted. Drude could then see no way49 for gravity to be linked to electricity and magnetism and so did not follow Stoney and Planck in devising natural units containing G. Even for Planck, the entry of G into his natural units was a mystery. He offered no explanation as to the meaning of the tiny Planck units of length and time. What did they mean? What would happen if you looked at the world on these dimensions? It would be a long time before these questions were asked50 and far longer before they were answered.
PLANCK GETS REAL
‘The increasing distance of the physical world picture from the world of the senses means nothing but a progressive approach to the real world.’
Max Planck
We have seen how Max Planck appealed to the existence of universal constants of Nature as evidence for the existence of a physical reality that was quite distinct from human minds. But he wanted to go much further and use the existence of these immutable constants as an argument against positivistic philosophers who thought science was entirely a human edifice: measured points organised in a convenient way by a theory that will eventually be replaced by a better one. Planck appreciated that the writing of equations and the formulation of physical theories was a human activity, but that does not mean that it is nothing but a human activity. For him, the constants of Nature had emerged uninvited and, as his natural units clearly showed, were not chosen for human convenience alone. He writes:51
‘These … numbers, the so-called “universal constants” are in a sense the immutable building blocks of the edifice of theoretical physics.
So now we must continue with the question: What is the real meaning of these constants? Are they, in the last analysis, inventions of the inquiring mind of man, or do they possess a real meaning independent of human intelligence?
The first of these two views is professed by the followers of positivism, or at least by its most extreme partisans. Their theory is that physical science has no other foundation than the measurements on which its structure is erected, and that a proposition in physics makes any sense only in so far as it can be supported by measurements.
Therefore, up to quite recently, positivists of all hues have also put up the strongest resistance to the introduction of atomic hypotheses and thereby also to the acceptance of the above mentioned universal constants. This is quite understandable, for the existence of these constants is a palpable proof of the existence in nature of something real and independent of every human measurement.
Of course, even today a consistent positivist could call the universal constants mere inventions which have proved to be uncommonly useful in making possible an accurate and complete description of the most diversified results of measurement. But hardly any real physicist would take such an assertion seriously. The universal constants were not invented for reasons of practical convenience, but have forced themselves upon us irresistibly because of the agreement between the results of all relevant measurements, and – this is the essential thing – we know quite well in advancethat all future measurements will lead to these selfsame constants.’
There were many more options open to Planck's opponents, of course. It might have been that the constants he chose were not truly constants at all when scrutinised with vastly greater precision.
1 comment