Le monde comme volonté et comme représentation Read Online

Si la métaphore n’était pas un peu risquée, et par suite légèrement ridicule, on pourrait, avec assez d’exactitude, comparer les concreta au rez-de-chaussée, et les abstracta aux étages supérieurs dans l’édifice de la réflexion(16).

Ce n’est point, comme on le dit trop souvent, un caractère essentiel, mais seulement une propriété secondaire et dérivée du concept, d’embrasser un grand nombre de représentations ou intuitives, ou abstraites, dont il est le principe de connaissance, et qui sont pensées en même temps que lui. Cette propriété, bien qu’elle existe toujours en puissance dans le concept, ne s’y trouve pas nécessairement en réalité ; elle repose sur ce fait que le concept est la représentation d’une représentation et doit toute sa valeur au rapport qu’il a avec cette autre représentation ; cependant le concept ne se confond pas avec elle ; car celle-ci appartient le plus souvent à une tout autre classe, à l’intuition, par exemple ; elle est soumise, comme telle, aux déterminations du temps, de l’espace et à beaucoup d’autres qui ne font pas partie du concept lui-même ; il s’ensuit que des représentations diverses qui n’offrent que des différences superficielles peuvent être pensées ou subsumées sous le même concept. Mais cette propriété que possède le concept d’être valable pour plusieurs objets ne lui est pas essentielle, elle est purement accidentelle. Il peut donc exister des notions sous lesquelles une seule chose réelle serait pensée ; elles n’en sont pas moins pour cela abstraites et générales, et ce ne sont nullement des représentations particulières et intuitives.

Telle est, par exemple, l’idée qu’on se fait d’une ville quand on ne la connaît que par la géographie ; on ne conçoit alors, à la vérité, qu’une seule ville, mais la notion qu’on s’en forme pourrait convenir à un grand nombre d’autres, différentes à beaucoup d’égards. Ainsi, ce n’est nullement parce qu’une idée est extraite de plusieurs objets qu’elle est générale ; c’est, au contraire, parce que la généralité, en vertu de laquelle elle ne détermine rien de particulier, lui est inhérente comme à toute représentation abstraite de la raison, c’est pour cela, dis-je, que plusieurs choses peuvent être pensées sous le même concept.

Il résulte de ces considérations que tout concept, étant une représentation abstraite et non intuitive, par suite toujours incomplètement déterminée, possède, comme on dit, une extension ou sphère d’application, et cela dans le cas même où il n’existe qu’un seul objet réel correspondant à ce concept. Or, la sphère de chaque concept a toujours quelque chose de commun avec celle d’un autre ; en d’autres termes, on pense, à l’aide de ce concept, une partie de ce qui est pensé à l’aide du second, et réciproquement ; toutefois, lorsque les deux concepts différent réellement, chacun ou au moins l’un des deux, doit comprendre quelque élément non renfermé dans l’autre : tel est le rapport du sujet au prédicat. Reconnaître ce rapport, c’est juger. Une des idées les plus ingénieuses qu’on ait eues a été de représenter à l’aide de figures géométriques cette extension des concepts. Godefroy Ploucquet(17) en eut vraisemblablement la première pensée ; il employait, à cet effet, des carrés ; Lambert, venu après lui, se servait encore de simples lignes superposées ; Euler porta le procédé à sa perfection en faisant usage de cercles. Je ne saurais dire quel est le dernier fondement de cette analogie si exacte entre les rapports des concepts et ceux des figures géométriques. Toujours est-il qu’il y a pour la logique un précieux avantage à pouvoir ainsi représenter graphiquement les relations des concepts entre eux, même au point de vue de leur possibilité, c’est-à-dire a priori.

Voici ces figures :

1° Les sphères de deux concepts sont rigoureusement égales : telle est, par exemple, la notion de nécessité et celle du rapport de principe à conséquence, ou encore l’idée de ruminants et celle de bisulques ; celle de vertébré et d’animal à sang rouge (on pourrait cependant contester cet exemple à cause des annélides) ; ce sont là des notions convertibles. On les représente alors par un cercle unique qui figure indifféremment l’une ou l’autre.

2° La sphère d’un concept renferme en totalité celle d’un autre concept.

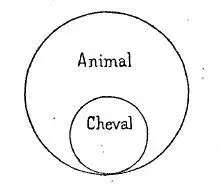
3° Une sphère en comprend deux ou plusieurs autres qui s’excluent tout en étant elles-mêmes contenues dans la grande.

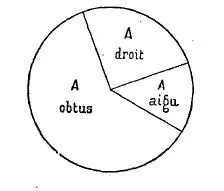
4° Deux sphères contiennent chacune une partie l’une de l’autre.

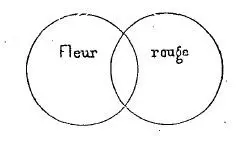
5° Deux sphères sont renfermées dans une troisième sans la remplir.

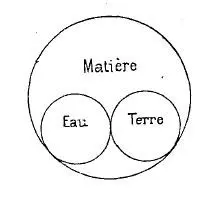
À ce dernier cas appartiennent les concepts dont les sphères ne communiquent pas directement, mais qu’un troisième concept plus étendu comprend dans sa circonscription.

Les diverses combinaisons possibles de concepts se ramènent aux cas précédents ; on en peut déduire toute la théorie des jugements : (conversion, contraposition, réciprocité, disjonction (cette dernière d’après la troisième figure) ; on en tirerait aussi bien les caractères des jugements, sur lesquels Kant a fondé ses prétendues catégories de l’entendement. Il faut cependant faire une exception pour la forme hypothétique, qui n’est pas une simple combinaison de concepts, mais bien une synthèse de jugements ; il faut également mettre à part la modalité, dont il sera traité expressément dans l’Appendice, ainsi que de tous les caractères qui ont servi de base aux catégories kantiennes.

Une dernière remarque à faire au sujet des diverses combinaisons de concepts dont on vient de parler, c’est qu’elles peuvent encore s’unir entre elles, par exemple la quatrième figure avec la seconde. Lorsqu’une sphère qui en comprend une autre, soit en totalité, soit seulement en partie, est à son tour contenue tout entière dans une troisième, cette combinaison représente le syllogisme de la première figure, synthèse de jugements qui permet d’affirmer qu’une notion contenue en totalité ou en partie dans une seconde l’est aussi dans une troisième, où celle-ci se trouve elle-même renfermée. Et de même si le syllogisme conclut négativement : la seule manière de le figurer alors est d’imaginer deux sphères dont l’une contient l’autre, exclues toutes deux d’une troisième. Lorsqu’un grand nombre de sphères s’emboîtent ainsi les unes dans les autres, on obtient les longues séries syllogistiques.

Ce schématisme des concepts a déjà été assez convenablement exposé dans plusieurs traités pour servir désormais de base à la théorie des jugements et à la syllogistique tout entière ; l’enseignement s’en trouve très simplifié et facilité. Toutes les règles, en effet, peuvent, par ce procédé, être comprises, déduites et rattachées à leur principe. Toutefois, il n’est pas nécessaire de charger la mémoire de cette foule de préceptes, car si la logique a un intérêt spéculatif pour la philosophie, elle est dépourvue d’utilité pratique. On peut dire, à la vérité, que la logique joue, à l’égard du raisonnement, le rôle de la basse continue en musique, ou, à parler moins exactement, le rôle de l’éthique par rapport à la vertu ou de l’esthétique par rapport à l’art. Il faut, d’ailleurs, reconnaître que l’étude de la science du beau n’a pas encore produit un seul artiste, pas plus que l’étude de la morale un honnête homme. Longtemps avant Rameau, ne composait-on pas de belle et bonne musique ? Il n’est pas nécessaire de posséder à fond la science de l’accompagnement pour reconnaître les dissonances ; il n’est pas besoin non plus de savoir la logique pour ne pas se laisser abuser par des paralogismes. On doit avouer pourtant que les règles de l’harmonie sont indispensables sinon à l’appréciation, au moins à la composition d’une œuvre musicale ; l’esthétique et l’éthique elle-même peuvent aussi, bien qu’à un moindre degré, avoir un intérêt pratique, d’un caractère, il est vrai, surtout négatif ; on ne doit donc pas leur dénier toute utilité. On n’en saurait dire autant de la logique. Elle n’est, en effet, que la forme abstraite d’une science que chacun possède à l’état concret. Aussi n’a-t-on guère besoin d’invoquer les règles de la logique, soit pour éviter un paralogisme, soit pour faire un raisonnement juste ; le plus grand logicien du monde les laisse complètement de côté lorsqu’il raisonne pour de bon. La cause en est facile à saisir : toute science consiste dans un système de vérités générales et, par suite, abstraites, dans un ensemble de lois et de règles relatives à une espèce déterminée d’objets. Chaque fait particulier de cet ordre qui se présente ensuite s’explique toujours par ces notions générales, dont la valeur a été reconnue une fois pour toutes ; il est beaucoup plus aisé, en effet, d’appliquer ainsi une règle commune à tous les cas, que d’en étudier un isolément pour en trouver l’origine : l’idée abstraite et générale, une fois acquise, est beaucoup plus abordable que l’étude empirique d’un phénomène particulier. Pour la logique, c’est juste le contraire. Elle est la science générale des procédés de la raison, analysés par la raison elle-même et érigés en préceptes à la suite d’une abstraction opérée sur la pensée. Mais ces procédés, elle les possède nécessairement et essentiellement ; elle ne s’en écartera donc jamais, du moment qu’elle sera abandonnée à elle-même.